A curious observer’s guide to quantum mechanics, pt. 4: Looking at the stars

One of the quietest revolutions of our current century has been the entry of quantum mechanics into our everyday technology. It used to be that quantum effects were confined to physics laboratories and delicate experiments. But modern technology increasingly relies on quantum mechanics for its basic operation, and the importance of quantum effects will only grow in the decades to come. As such, physicist Miguel F. Morales has taken on the herculean task of explaining quantum mechanics to the rest of us laymen in this seven-part series (no math, we promise). Below is the fourth story in the series, but you can always find the starting story plus a landing page for the entire series thus far on site.

Beautiful telescopic images of our Universe are often associated with the stately, classical physics of Newton. While quantum mechanics dominates the microscopic world of atoms and quarks, the motions of planets and galaxies follow the majestic clockwork of classical physics.

But there is no natural limit to the size of quantum effects. If we look closely at the images produced by telescopes, we see the fingerprints of quantum mechanics. That’s because particles of light must travel across the vast reaches of space in a wave-like way to make the beautiful images we enjoy.

This week we’ll concentrate on how photons travel across light years, and how their inherent quantum waviness enables modern telescopes, including interferometric telescopes the size of the Earth.

Starlight

How should we think about the light from a distant star? Last week we used the analogy of dropping a pebble into a lake, with the ring of ripples on the water standing in for the wave-like motion of photons. This analogy helped us understand the length of a particle ripple and how photons overlap and bunch together.

We can continue that analogy. Every star similar to the Sun, in that it makes a lot of photons. As opposed to someone carefully dropping single pebbles into a mirror-smooth lake, it’s more like they poured in a bucket of gravel. Each pebble makes a ring of ripples, and the ripples from each stone spread out as before. But now the ripples are constantly mixing and overlapping. As we watch the waves lap against Earth’s distant shore, we don’t see the ripples from each individual pebble; instead the combination of many individual ripples have added together.

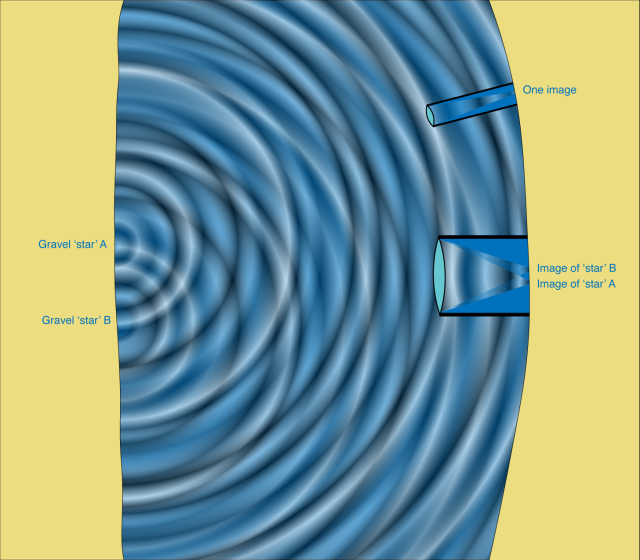
So let’s imagine we’re standing on the shore of a lake as the waves wash in, looking at our gravel ‘star’ with a telescope for water waves. The lens of the telescope focuses the waves from the star onto a spot: the place on the camera sensor where the light from that star lands.

If a second bucket of gravel is dropped into the lake farther along the opposite shore, the ripples will overlap at our shore, but will be focused by the telescope into two distinct spots on the detector. Similarly, a telescope can sort the light from the stars into two distinct groups—photons from star A and photons from star B.

But what if the stars are very close together? Most of the ‘stars’ we see at night are actually double stars—two suns so close together they appear as one bright pinprick of light. When they’re in distant galaxies, stars can be separated by light years yet look like a single spot in professional telescopes. We’d need a telescope that could somehow sort the photons produced by the different stars to resolve them. Similar things apply if we want to image features like sunspots or flares on the surface of a star.

To return to the lake, there is nothing special about the ripples made by different pebbles—the ripples from one pebble are indistinguishable from the ripples made by another. Our wave telescope does not care if the ripples came from different pebbles in one bucket or different buckets altogether—a ripple is a ripple. The question is how far apart must two pebbles be dropped for our telescope to distinguish that the ripples came from different locations?

Sometimes when you’re stumped, it’s best to take a slow walk along the beach. So we’ll have two friends sit on the far shore dropping pebbles, while we walk along our shore, looking at the waves and thinking deep thoughts. As we walk along the beach we see that the waves from our friends overlap everywhere, and that the waves come in randomly. There appears to be no pattern.

But on closer inspection, we notice that spots on the beach very near each other see nearly identical waves. The waves are random in time, but locations on the beach a few paces apart see the same random train of waves. But if we look at waves hitting far down the beach, that wave train is completely different than the one hitting near us. Any two places on the beach that are close together will see nearly identical wave trains, but widely separated locations on the beach see different wave trains.

This makes sense if we think of the waves on the beach as being the combination of little ripples from hundreds of pebbles. At nearby locations on the beach, the ripples from the pebbles dropped by both friends add up in the same way. But farther along the beach, the ripples from one friend will have to travel farther, so the ripples add up in a different way, giving us a new wave train.

While we can no longer see the ripples of individual pebbles once they have combined into waves, we can pace off how far we need to walk to see a new wave train. And that tells us something about how the ripples are adding together.

We can confirm this by asking our two pebble-dropping friends to move closer together. When our friends are close together, we notice that we have to walk a long way along our beach to see the ripples add up in a different way. But when our friends are far apart, just a few steps on our beach will make the wave trains look different. By pacing off how far we need to walk before the waves look different, we can determine how far apart our pebble-dropping friends are.

The same effect happens with photon waves, which can help us understand the resolution of a telescope. Looking at a distant binary star, if the light waves entering opposite edges of the telescope look different, then the telescope can sort the photons into two distinct groups—the photons from star A and the photons from star B. But if the light waves entering opposite edges of the telescope look the same, then the telescope can no longer sort the photons into two groups and the binary star will look like one spot to our telescope.

If you want to resolve nearby objects, the obvious thing to do is to make the diameter of the telescope bigger. The farther apart the edges of the telescope, the more close the stars can be and still be distinguished. Bigger telescopes have better resolution than small telescopes, and can separate the light from more closely spaced sources. This is one of the driving ideas behind building truly enormous 30 or even 100 meter diameter telescopes—the bigger the telescope, the better the resolution. (This is always true in space, and true on the ground with adaptive optics to correct for atmospheric distortions.)

By Miguel F. Morales